The No-Data Algorithm
Enabling trust in LLMs-as-judges WITHOUT labelled data
This is the TL;DR of my paper Labelling Data with Unknown References. If you are looking for the code, it is here.
We have a huge problem: evaluating highly-capable LLMs is expensive. Using an LLM as labeller (i.e., LLM-as-judge) is becoming quite common, but the field is VERY divided on their effectiveness and feasibility. Add to that lack of data and pressure to scale, and you're in a pickle.
There are three ways you can prove that a labeller works: statistics (which won't work without data), faith (which is not science), or a formal proof. I introduce here an algorithm that (via a formal proof, obviously) allows you to decide if you can trust your LLM-as-judge in a mathematically rigorous manner.
Outline
- The TL;DR
- The No-Data Algorithm
- Sketches of the proofs
- Some experimental results!
- Implications and conclusion
- It is possible to label data without having any labels, provided that the 'thing' saying 'hey I know the labels!' (an LLM) proves it can be trusted.
- This means that an LLM-as-judge can be trusted to be a labeller iff it passes the checks from the No-Data algorithm. It judges the judges, if you will, in a mathematically rigorous manner.
- In turn this suggests that we do not need labelled data to establish trust. As per this site (obviously AI-generated but a great summary; and they do say that humans check it), this has applications where this data is scarce (healthcare, market research, low-resource languages, etc), but models (LLMs) trained with lots of internet data COULD perform well.
Picture this: You do not know how to solve a problem, but someone says they can, and they tell you 'just trust me, bro'.
As a (self-respecting) scientist, that is not an argument that we should accept. Especially from a machine without provable guarantees of convergence (or at least, ill-characterised). So how do you decide if you can trust it?
Usually, this is done via one of three arguments. The first, is a statistical argument (i.e., a test set). But you do not have that, or the benchmarks are too contaminated, and hence you cannot possibly know the true answer--perhaps nobody can. The second would be via faith (the 'just trust me, bro' argument), which as we established, is not science. The third would be a formal proof.
Enter the No-Data Algorithm. Granted, it is technically the 'no-labels algorithm', but since you do not have labelled data, it can go either way. The point is, I claim that this algorithm can enable you to establish trust in an evaluator (say, an LLM) even when you do not have labelled data.
Does it work?
Yes!
How?
Just trust me, bro.
Ok, not really. This post will introduce the algorithm and sketches of the proof. There's some experimental results, too, because peer-reviewers usually won't be convinced by proofs alone; and because it turns out that empirically, under realistic scenarios, there are some deviations from the theory that are quite interesting to look at.
The No-Data Algorithm works as follows: you have (unlabelled) data, and a rubric of what the labels should be. For example, it could be something like 'does the summary cover at least five keypoints of the original text?' or 'does this string contain an even number of zeros?'.
An Evaluator claims it knows the labels. A Verifier must check the labels of the evaluator, but without knowing the labels. What this algorithm does is that, via a protocol (kind of like a game) called the EV Protocol, gets the Evaluator and Verifier to talk to each other until the Verifier says whether it is sufficiently convinced (or not) about the Evaluator's performance.
You then run the EV Protocol on your entire dataset and get a labelled dataset and a statement on whether these labels can be trusted, and to what extent. If the Verifier is not convinced, you then also have a chance to flip the label given by the Evaluator.
Here's a picture of the algorithm.

As you probably guessed, the important bit is the EV Protocol. This is motivated by classic results in computational complexity theory, such as the Arthur-Merlin protocol from Babai, and it is a type of zero-knowledge proof. This is why the No-Data Algorithm is mathematically rigorous secure, by the way. What a zero-knowledge proof is (formally) is beyond the scope of this post, but the gist of it is that it establishes trust via challenges. They are used in blockchain, authentication systems, and other critical areas where you should not ever assume that the interlocutor (in this case, the Evaluator) is telling the truth.
The EV Protocol has two challenges designed to provide sufficient and necessary information as to whether you can trust your labeller. I'll explain why they are sufficient and necessary in the next section. Here I'll introduce them, but first let me explain the rest of the protocol.
The protocol works as follows:
- Given a datapoint \(x\) and the rubric \(C\), the Evaluator comes up with a new datapoint \(\tilde{x}\) that, according to it, will lead to the same label.
- The Verifier selects, uniformly at random, one of two challenges:
- Does \(\tilde{x}\) have the evaluation under \(C\) as \(x\)?, or
- Does \(\tilde{x}\) have the same structure as \(x\)?
- IF the Evaluator passes the challenge, you go back to (1) and start all over. Repeat \(r\) times.
We can show that if the Evaluator can lie or cheat to pass one of the challenges, then the probability that the Verifier will succeed at catching a lying Evaluator will be \(1 - 1/4^r\), or around 98% for \(r=3\). In fact, we will also show if the challenges are consistent and complete (i.e., sufficient and necessary), being able to pass both challenges for any choice of \(\tilde{x}\) means that the Verifier knows the labels. So, conversely, not passing the challenges consistently = lying.
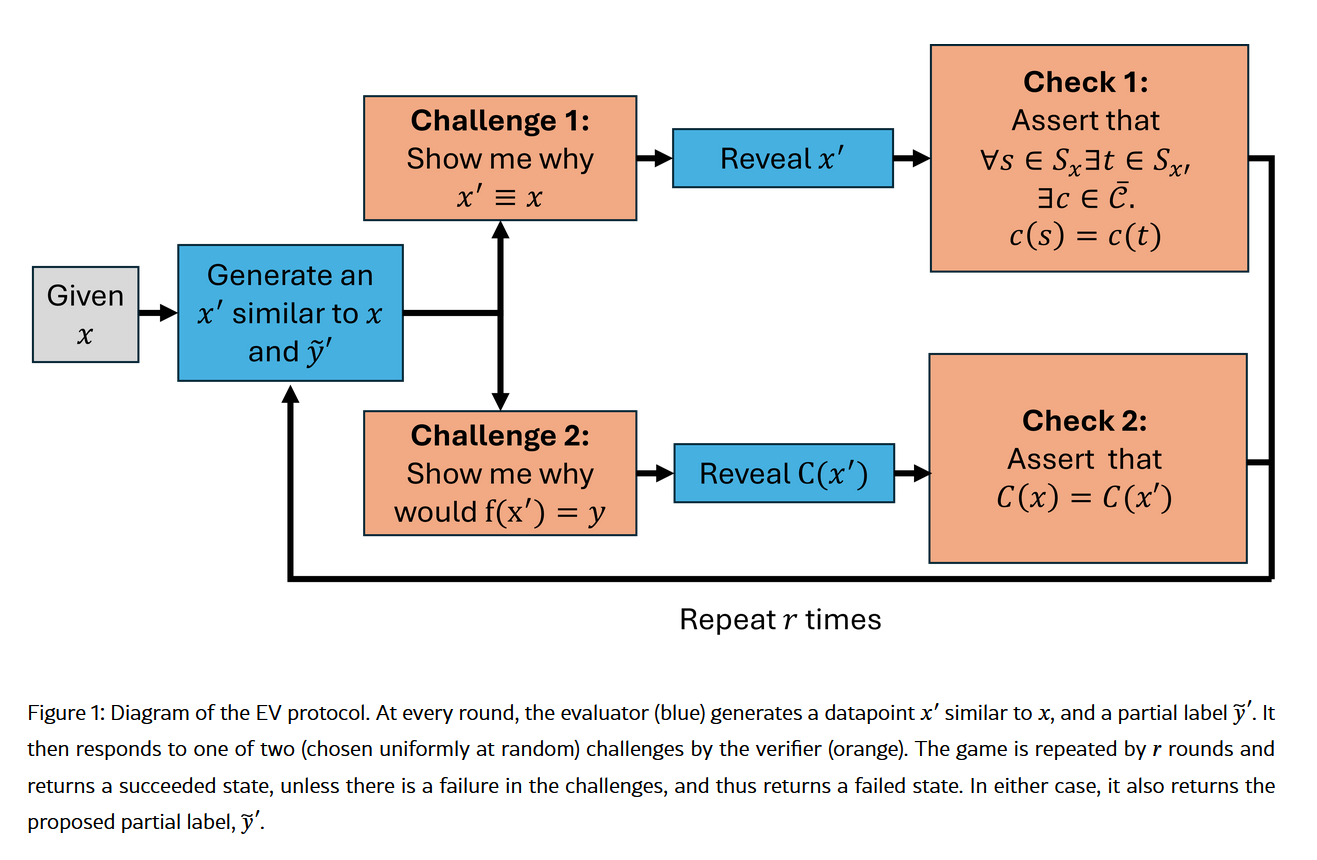
Before we get to the proofs, let me just repeat what we do:
- We (the Verifier, rather) challenge the Evaluator on every point that must be labelled. If it passes the challenge, we accept it. If it fails it, we reject it.
- The challenges are designed to catch liars, so it is possible for us (with a bounded probability) to establish confidence on our evaluator without the need of labels.
We'll do a very short sketch of the proofs--don't worry, this is more to understand why it works. If you are interested in the full proofs, check out the paper.
The plan: to prove correctness of the No-Data algorithm we need two things:
- Correctness of the EV protocol, and
- (as a corollary) correctness of the full algorithm.
We'll start with the EV protocol, and namely that it is sufficient and necessary. For this, note that the rubric \(C\) is a checklist for your labels, but not the final 'decider' of these labels. After all, the way you aggregate the answers to the checklist is what decides the label, not the other way around (for example, majority vote, a non-linear function, best-of-3, etc). Let's call that \(\sigma\). It is easy to argue that your final label \(y\) will be done by first passing \(x\) into \(C\), and then this output into the aggregator: \(y = \sigma C(x)\). Let's assume that \(\sigma\) is a deterministic function.
So, nobodody knows \(\sigma\), but everyone knows \(C\). Then the checks will (should) focus on ensuring that \(C\) leads to the same valuation \(C(x)\) for any newly-generated \(\tilde{x}\). However, there are many ways one can get the same output valuation \(C(x)\) (for example, by having multiple points checking the same boxes), but that does not mean that \(x\) and \(\tilde{x}\) are equivalent!!!.
Why not? Because if \(C\) has many linear terms, like 'if this, label should be 1, otherwise 0', all valuations will be the same. But with non-linear terms, like 'if this or that, then 0, otherwise 1', the \(\tilde{x}\) point that the Evaluator generates could get lucky and fulfil the 'this' or 'that' in the non-linear term--no guarantee that we are looking at the same point as \(x\).
So we need to check for same valuation (\(C(x) =? C(\tilde{x})\)), as covered in Challenge 1 from the previous section, but also whether the points are structurally the same (to account for luck) (which is Challenge 2, above). Crucially, knowing Challenge 1 does not give information about Challenge 2, and viceversa. Which in turn means that being able to solve Challenge 1 (r. 2) does not necessarily mean solving the entire thing, but solving the entire thing does mean knowing Challenges 1 and 2. Hence both challenges are sufficient and necessary.
Now, about completeness: since every challenge is chosen uniformly at random, Challenge 1 and Challenge 2 have both the same probability of appearing in front of the Evaluator. A lying Evaluator may only be able to pass one of the challenges (as per above: passing both means knowing the actual label), and sure, it can prepare in advance, but it does not know in advance which one it will see. So the probability of getting lucky when lying is \(1/4\). It is also easy to show that this is the worst case scenario. Repeat this \(r\) times, and you get a probability of failure (by the Verifier) of \(1/4^r\).
From the above, it follows that the EV Protocol bounds, up to a tight probability, confidence on a labeller per datapoint. The expensive bit is that it does cost more times to run (by a factor of \(r\)), but on the other hand it allows you to label data iff the Evaluator knows it (more on that later!).
These are super short because I think the paper conveys the work better. The gist of it is that I ran two experiments: one to show that the empirical results adjusted to the theory; and another with an application (low-resource data classification!).
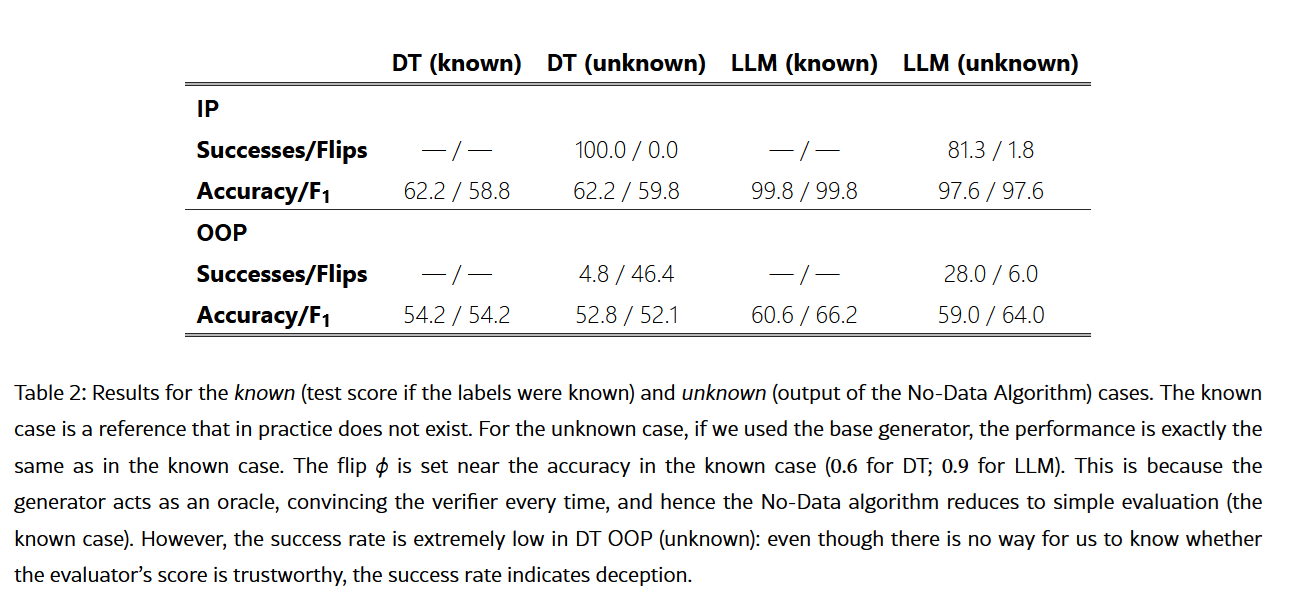
For the empirical study, I created a synthetic data to illustrate the point, using both a decision tree and an LLM-as-a-judge (o3-mini) as evaluators, and a regex as verifier. It evaluated a problem it did know (in-phenomenon, or IP) as well one it claimed it did (but actually didn't, out-of-phenomenon or OOP). I split the cases in 'knowable' and 'unknowable', where 'knowable' is, as per the title of this paper, not something we handle and is just there to illustrate what the 'true' accuracy would be if we knew the real label set.
The predictions of the paper adjusted quite well, with the LLM and the decision tree lying through their teeth (and being caught) when the setup required it (the OOP case); and successfully (impressively, I might add, for o3-mini) solving the IP case. The paper has further studies on DeepSeek, Qwen 2.5B, and GPT-4o. Check it out if you're interested.

For the low-resource study, I chose West Frisian. It is close to my heart and I think that it deserves more attention. Even when it is spoken by about half a million people, those who know how to write it are even fewer. Hence, as per the taxonomy of Joshi et al., it is an extremely low-resource language, where--as called out in the paper for many languages--synthetic data will do more harm than good. Hence, it is a great case study! Can you enable others to work on scarce data scenarios? Here, 'enable' means 'they can trust the tool they are using'.
So for this one I got native speakers to translate a multi-domain dataset (MMLU, OpenOrca, WildChat, and OpenCode) of prompts and outputs. Both the Evaluator and the Verifier are LLMs (GPT-4.1).
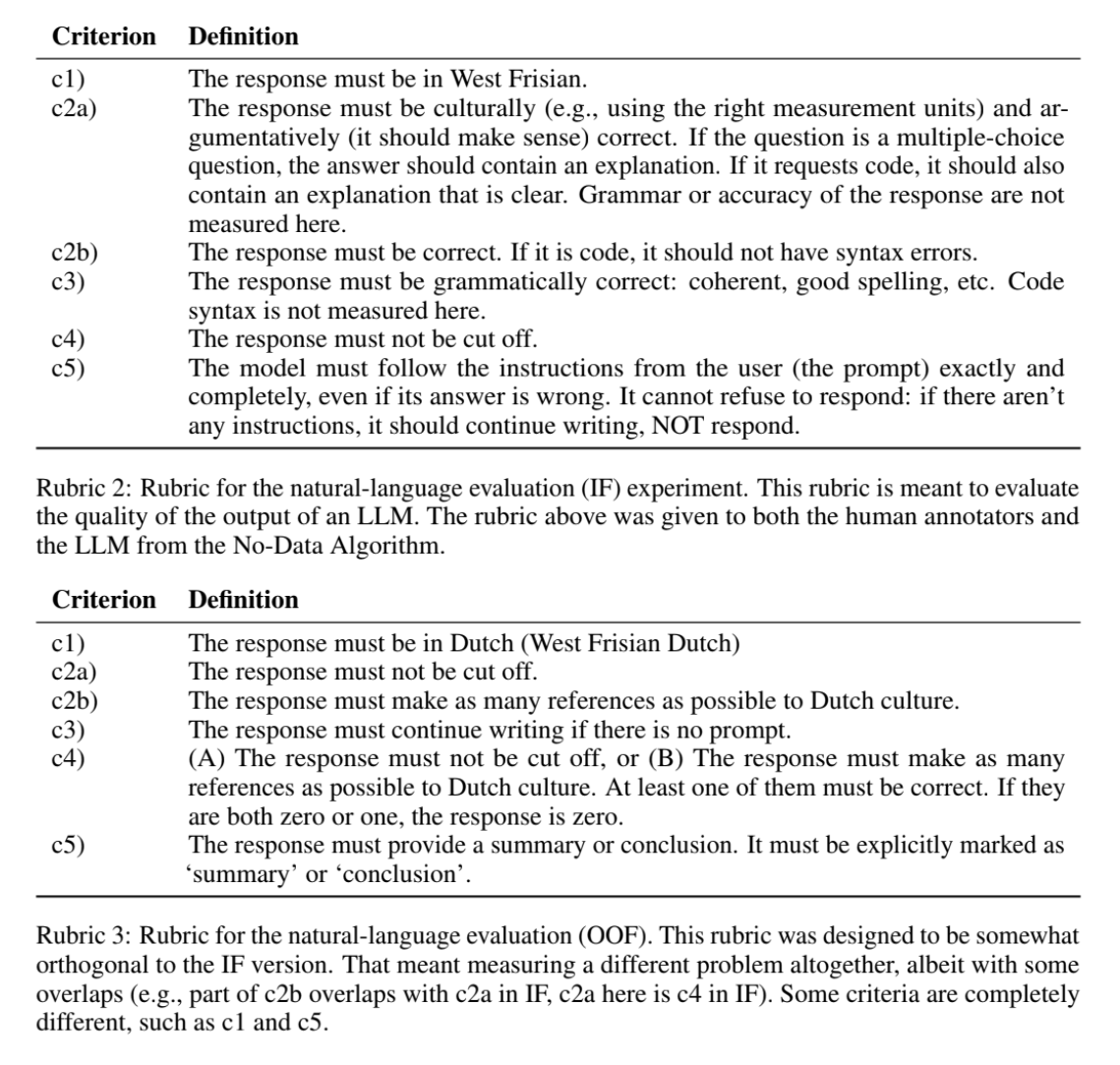
The task for the LLM-as-judge was to evaluate whether the output was 'good' with respect to a rubric (below).
The task for the No-Data Algorithm was to judge the judge to determine trustworthiness. So I created a separate rubric (also below) to determine how and when a model would lie. Lo and behold, the results stuck to the theory, with the LLM-as-judge showing near-random performance when the data was OOP, and somewhat okish performance in IP. Crucially, in this experimeent the values of the rubric were unknown; and the LLMs had to label it themselves!
The setup, however, was slightly different than the theoretical work: for example, in the empirical test the criteria was evaluated by an oracle, while here both LLMs need to score the criteria first, and then do the whole EV protocol. There was also the matter of LLMs doing whatever they want (because they are machines, they really really don't know what you are talking about). So, for example, if you put exemplars in the prompt, the LLMs will never pass any challenge. Turns out that they were lying for both IP and OOP, and the No-Data algorithm caught that!!it took me two weeks to figure out why the algorithm kept saying this
Of course, after removing the exemplars, things made more sense. But that took me a while to debug. Turns out that the outputs for every single criterion were almost the same, because it was mimicking the exemplars and not listening to the prompt. See what I mean about them not knowing what you are talking about?
It is interesting--while it could be argued that verifying an evaluator that is also a verifier leads to a circular argument, do note that these are two different problems. And, in fact, empirically the results reflected so. Plus if you are icky about it just use another model lol it's not like there is only one LLM out there.
Anyway, the takeaway is that we can use the No-Data Algorithm to label data in low-resource languages! And, more importantly, in realistic scenarios .
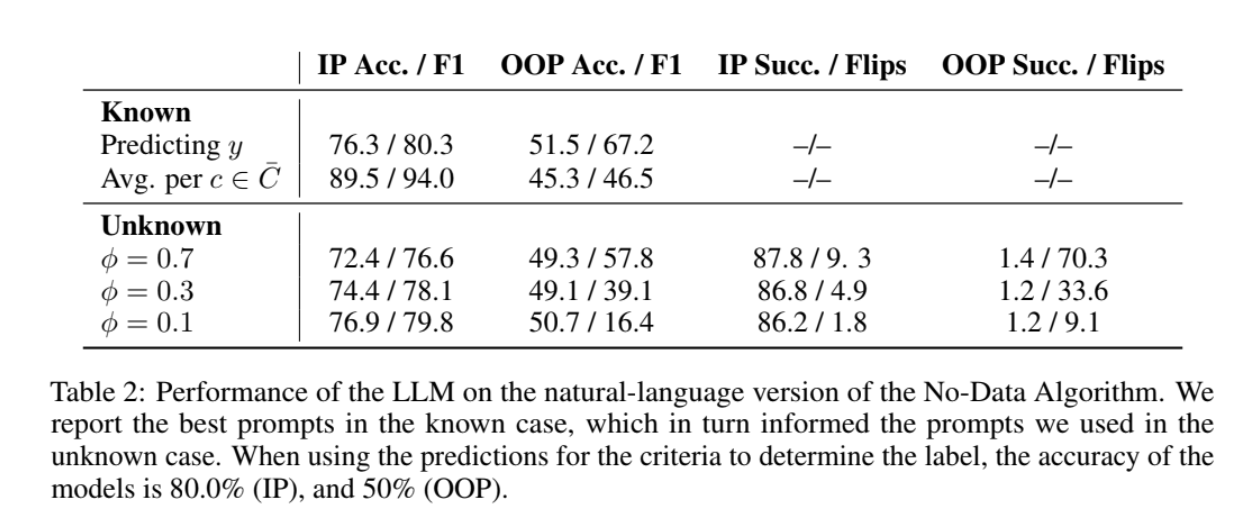
There is something cool, too. So far we have set up the problem so that one of the evaluators lies. What if it's not lying, just wrong? Well, the No-Data algorithm can also catch that: low success rates (like, really low) mean deception, but sort-of-low indicate lack of knowledge. For this I compared GPT-4.1 (which kinda knows West Frisian) with Qwen 2.5B (which definitely does not know West Frisian). See the table below for the results.
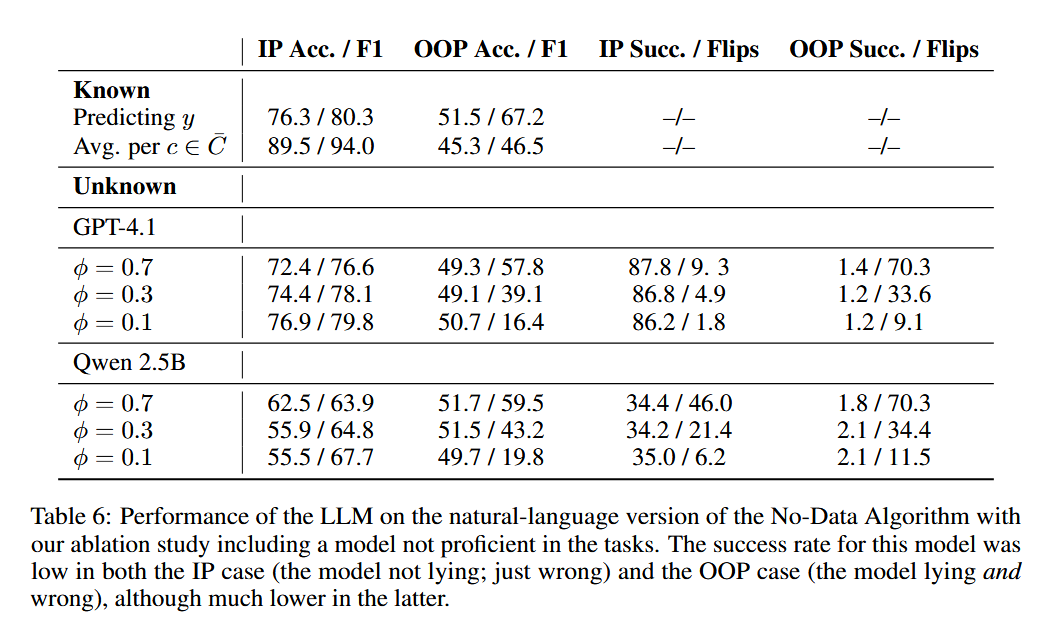
So what have we learnt?
- It is indeed possible to establish trust in an LLM-as-a-judge, even if you do not know the labels! This does not mean that you can just use them: what the No-Data algorithm says is 'you likely can/cannot trust this LLM in this task'. These challenges are mathematically rigorous. As in, they are proven to be what you need.
- You can get a labelled dataset with slightly better performance (slightly!!) if you flip the labels when you cannot trust the evaluator. It's not super duper useful, and frankly I would just stick to the No-Data algorithms measure of success.
Aside, what I believe is most interesting is the case when the Evaluator does not know the label: you can flip it as much as you'd like, and all you'll get is background noise on aggregate. So you aren't really violating any laws of nature: the entropy of the system remains unchanged! (little physics joke for you and yes I know that measurement will affect the information content of the system it is a joke chill)
The middle ground--when it gets some right and some wrong--is also why the No-Data algorithm only gives you a number: the successes. Everything else (including the threshold at which you are willing to trust a noisy evaluator) is up to the scientist. This is more or less how we are handling natural-language problems (for which this algorithm also works, as seen). What matters, really, is that the No-Data algorithm enables you to use LLMs-as-judges in areas where labelled data is extremely scarce, like market research, healthcare, and low-resource languages.
Speaking of, one of the cool bits about the No-Data algorithm applied to judging LLMs-as-judges is that, yes, it does work, but it establishes trust in the prompt, not the LLM. So there is room for improvement: how can we establish trust in the model? It'll likely be more expensive and have to be a meta-meta evaluator (since the No-Data algorithm is technically a meta-evaluator), but it could create extremely reliable, cryptographically-secure online benchmarks of performance for LLM competitions that cannot be gamed.
Adrian de WynterJuly 2025